
The value that is generated from the kriging process for any actually sampled location will be equal to the observed value at this point, and all the interpolated values will be the Best Linear Unbiased Predictors (BLUPs). The kriging predictor is an “optimal linear predictor” and an exact interpolator, meaning that each interpolated value is calculated to minimize the prediction error for that point. This helps to reduce bias in the predictions.
Clustering of points is also taken into account, so that clusters of points are weighted less heavily (in effect, they contain less information than single points). In a general sense, the kriging weights are calculated such that points nearby to the location of interest are given more weight than those farther away. Kriging also generates estimates of the uncertainty surrounding each interpolated value. It differs from simpler methods, such as Inverse Distance Weighted Interpolation, Linear Regression, or Gaussian decays in that it uses the spatial correlation between sampled points to interpolate the values in the spatial field: the interpolation is based on the spatial arrangement of the empirical observations, rather than on a presumed model of spatial distribution. An example of a value that varies across a random spatial field might be average monthly ozone concentrations over a city, or the availability of healthy foods across neighborhoods. Kriging is one of several methods that use a limited set of sampled data points to estimate the value of a variable over a continuous spatial field. We illustrate the method using a large set of MET data from a South Australian barley breeding program.Kriging is a method of spatial interpolation that originated in the field of mining geology as is named after South African mining engineer Danie Krige. The model can be regarded as a random effects analogue of AMMI (additive main effects and multiplicative interactions).
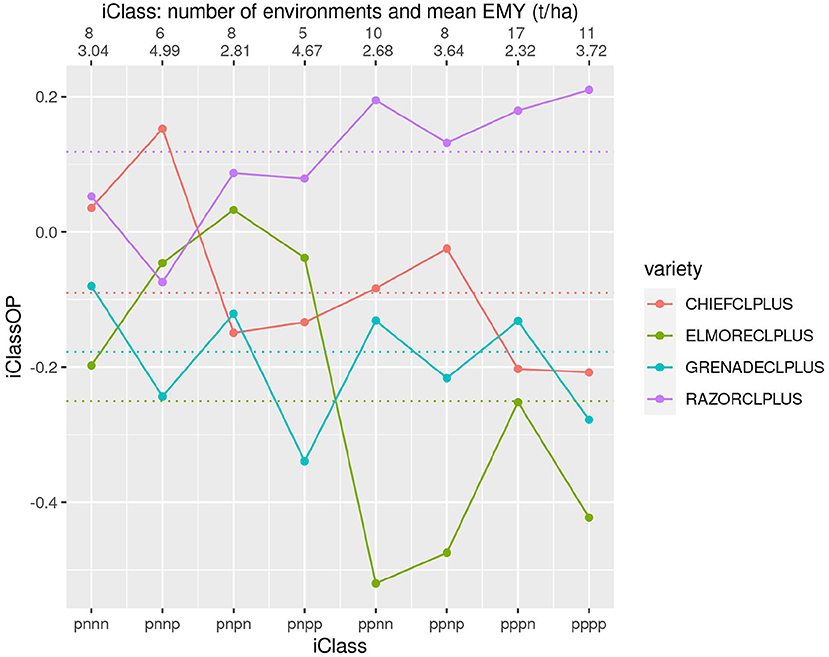
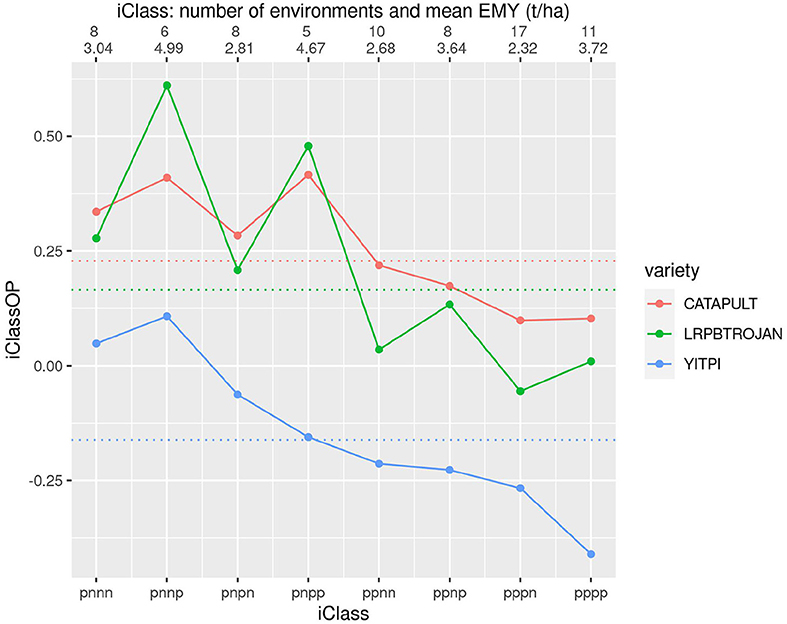
It allows a separate genetic variance for each environment and provides a parsimonious and interpretable model for the genetic covariances between environments. The multiplicative model corresponds to that used in the multivariate technique of factor analysis. In this paper we extend the analysis to include multiplicative models for the variety effects in each environment. Cullis, Cogel, Verbyla, and Thompson (1998) presented a spatial mixed model approach for the analysis of MET data. This information is obtained from series of plant variety trials, also known as multi-environment trials (MET). The recommendation of new plant varieties for commercial use requires reliable and accurate predictions of the average yield of each variety across a range of target environments and knowledge of important interactions with the environment. Analyzing variety by environment data using multiplicative mixed models and adjustments for spatial field trend.


 0 kommentar(er)
0 kommentar(er)
